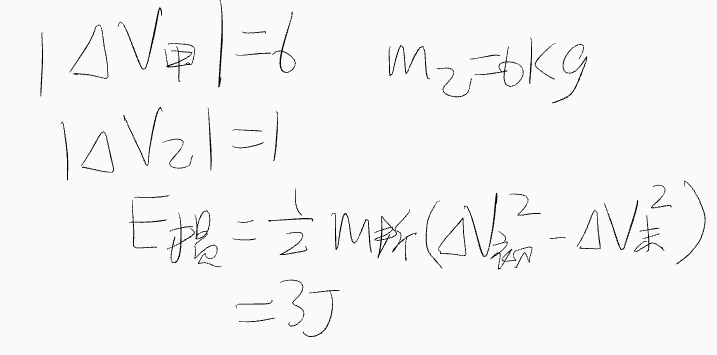Momentum

Perfect Elastic Collision

\( m_1 v_1 + m_2 v_2 = m_1 v_1' + m_2 v_2' \)

\( \frac{1}{2} m_1 v_1^2 + \frac{1}{2} m_2 v_2^2 = \frac{1}{2} m_1 v_1'^2 + \frac{1}{2} m_2 v_2'^2 \)

Procedure

1. \( v = \frac{m_1 v_1 + m_2 v_2}{m_1 + m_2} \)
2. \(v_1\), \(v\) and \(v_1'\) form an arithmetic sequence. \(v_2\), \(v\) and \(v_2'\) form another arithmetic sequence. (\( v - v_1 = v_1' - v \) and \( v - v_2 = v_2' - v \))

Perfectly inelastic collision

\( m_1 v_1 + m_2 v_2 = (m_1 + m_2) v' \)

Procedure

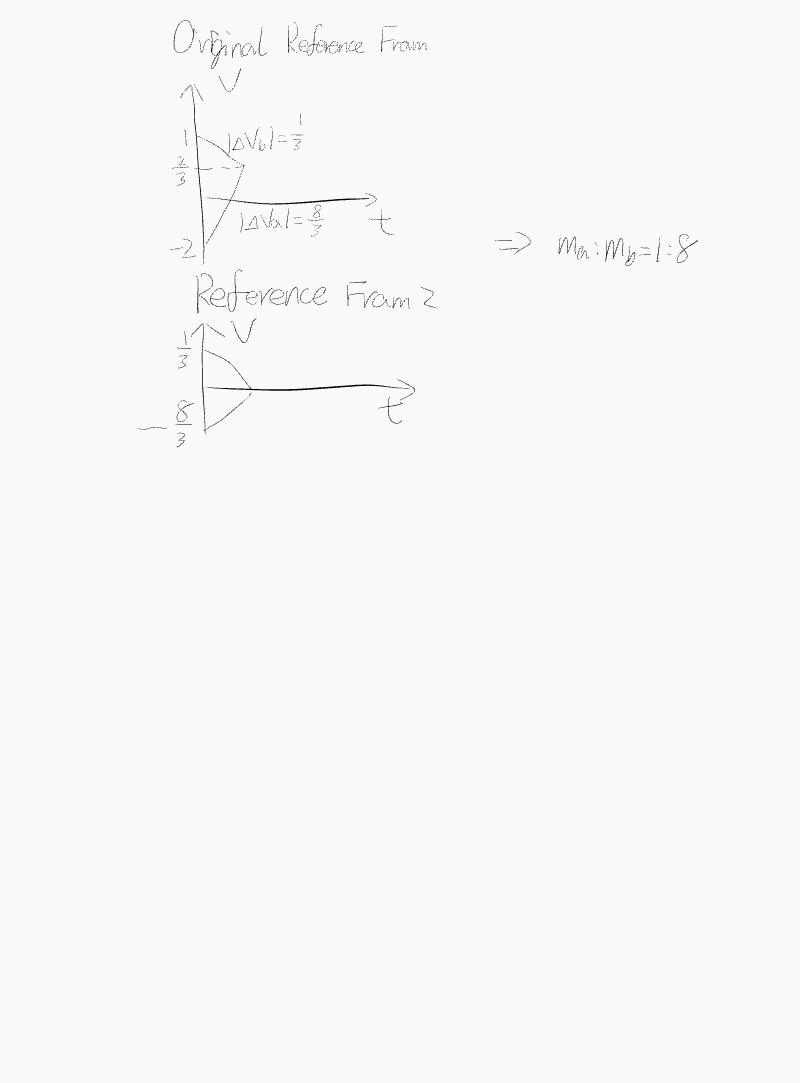
• \( Q = \frac{1}{2} \frac{m_1 m_2}{m_1 + m_2} (v_1 - v_2)^2 \) (Available energy, deduced from König's theorem)
• Use a special reference frame in which total momentum is zero.

Recoil

Requirement: The total momentum is zero.

Procedure

• Momentum and impulse are equal and opposite.
• \( \frac{a_1}{a_2} = \frac{v_1}{v_2} = \frac{x_1}{x_2} = \frac{E_{k1}}{E_{k2}} = \frac{m_2}{m_1} \)

Collision multiple times

Procedure

• For any collision occurring in an isolated system, momentum is conserved.
• One people throwing a ball at a wall \( I' = I = (2n - 1) m v \) ; \( I' = M v_n \)
• Two people throwing a ball at each other \( I_1 = (2n - 1) m v \) ; \( I_2 = 2n m v \)

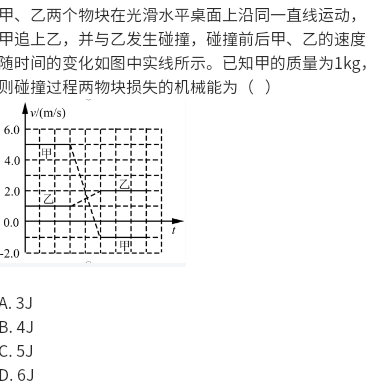
NCEE

Inelastic collision

Procedure

• \( E_{loss} = \frac{1}{2} \frac{m_1 m_2}{m_1 + m_2} (\Delta v_a^2 - \Delta v_b^2) \) (\( \Delta v_a \): Before collision; \( \Delta v_b \): After collision)

NCEE