AIinNCEE: An Introduction to essentials used in the National College Entrance Examination of the the People's Republic of China, A Great Involution
This book is dedicated, in respect and admiration, to the machines that works in the examination.
Preface
For over a decade, I have been basically killing my time, paying little attention to the class, and leaving homework undone whenever possible. This is because a school is never a place for learning knowledge and it can only deprive me of sleep. I have never attached enough importance to grades or entering a higher school. Now I have only one way to enter a university in China mainland, which is purely getting enough grades in the National College Entrance Examination. 90% is barely enough to enter a average university, and I think 95% is sufficient for me.
Occupied with doing research on NCEE, I basically stopped learning, researching and creating other things.
Foreword
Gross domestic product, Engel's coefficient, Wealth, Grades in education. Products, students, lifespan, air, virus, cities and some societies are compared with some accurate figures. Widespread use of figures employs a succession of gamesmanship and people devoted to it, referred to as machines. To appreciate getting grades as an intellectual activity in its own right you must turn to examination-oriented learning; you must read and firmly remember and use rules, facts and some models, and finally forget them after a short period of time. It doesn't matter much whether they are true or what applications they serve. What does matter is how well you brain perform just like a database or a machine running machine learning algorithms and how smoothly you fit with other people in the creation of a great civilization. The learner must seek both perfection of part and adequacy of collection.
The author
204 days before the final examination
Chemistry
Chemical equilibrium
Overall concentration changes
Increasing the concentration of the reactants is equivalent to increasing the pressure.
\( K_c \)
Procedure
- When the gas coefficients on both sides of the reaction equation are equal, \( V \) can be canceled, that is one can use \( n \) instead of \(c \).
NCEE

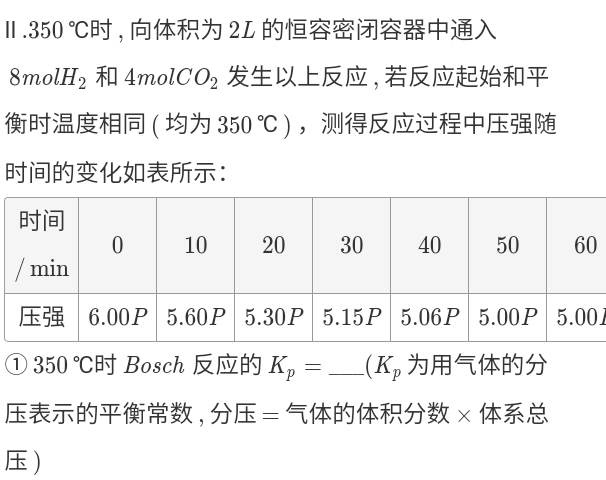
\( K_p \)
Procedure
- Sometimes \( p \) is proportional to \( n \) (\(p V = n R t \))
- \( K_p = \frac{p(C)^c p(D)^d}{p(A)^a p(B)^b} = \frac{(p \cdot x(C))^c (p \cdot x(D))^d}{(p \cdot x(A))^a (p \cdot x(B))^b} = p^{(c + d) - (a + b)} \frac{x(C)^c x(D)^d}{x(A)^a x(B)^b} \) (\(x \) is Mole fraction)
Constant pressure
NCEE
1
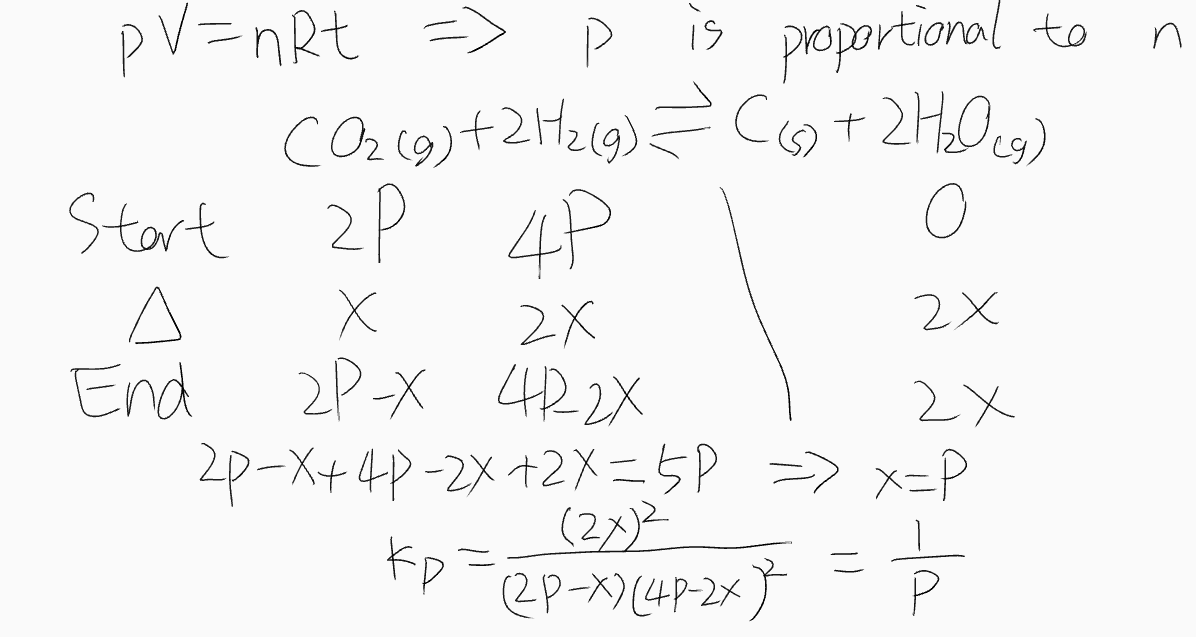
\( N_2 + 3H_2 \rightleftharpoons 2NH_3 \)
\( \frac{3-x}{6-2x} \) = 2
Conservations in Solutions
Charge conservation
Sign: no molecule, only ions
NCEE

Procedure 1
If \( c(A^+) + c(B^+) = c(C^-) + c(D^-) \)
\( c(A^+) > c(B^-) > c(C^+) > c(D^-) \) and \( c(A^+) > c(C^+) > c(B^-) > c(D^-) \) are false
In other word, The first and last ion must be both positive or both negative.
NCEE

Conservation of Matter
Sign: has ions and molecules; no \( H^+ \) \( OH^- \)
Conservation of protons
Sign: has ions and molecules and \( H^+ \) and \( OH^- \)
Extra: Concentration comparison
Major forms > Primary hydrolysis products and Primary ionization products > others
\( MA : HA = 1 : 1 \)
Either \( c(HA) > c(M+) > c(A^-) \) or \( c(A^-) > c(M+) > c(HA) \) is true
Maximum number of coplanar atoms
The only case where all atoms are not coplanar is saturated carbon atoms. A saturated carbon atom is a carbon atom that has only single bonds between other atoms.
Procedure
- Locate saturated carbon atoms
- Cut out 2 bonds in the principle of maximizing the number of atoms remaining
Exercise
How many maximum number of atoms are coplanar in
Extra: Asymmetric carbon
some  with branch chains
with branch chains
Organic
Procedure
- Degree of unsaturation: C + 1 + N/2 – H/2 – X/2 Wikipedia
Aldehydes and Ketones
Mnemonic
-
\( \require{AMScd} \begin{CD} RCHO + 2 Ag(NH_3)_2OH @>{\Delta}>> H_2O + 2Ag \downarrow + 3NH3 + RCOONH_4 \end{CD} \) \( \begin{CD} RCOONH_4 @>{H^{+}}>> RCOOH \end{CD} \)
-
\( \begin{CD} RCHO + 2 Cu(OH)_2 + NaOH @>{\Delta}>> Cu_2O \downarrow + 3 H_2O + RCOONa \end{CD} \) \( \begin{CD} RCOONa @>{H^{+}}>> RCOOH \end{CD} \)
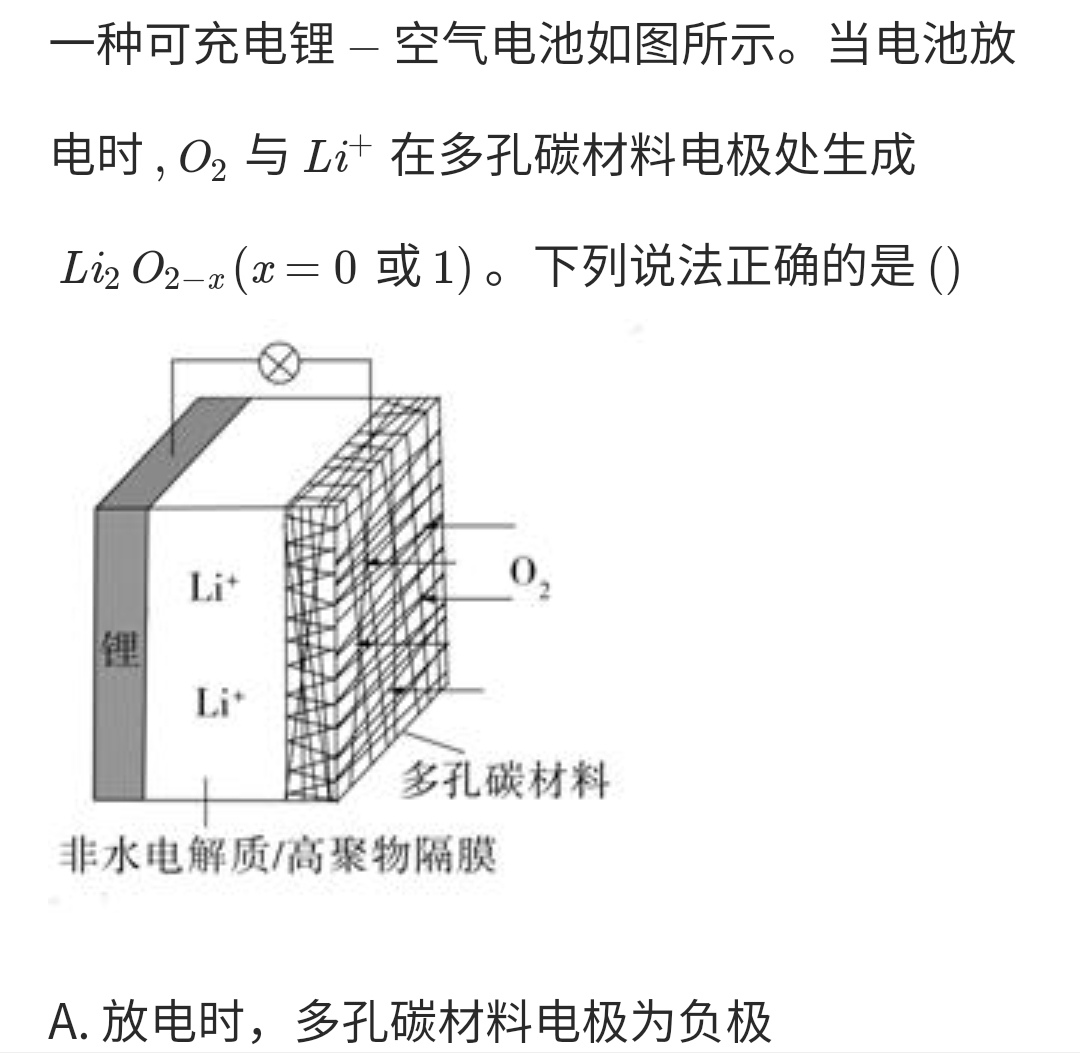
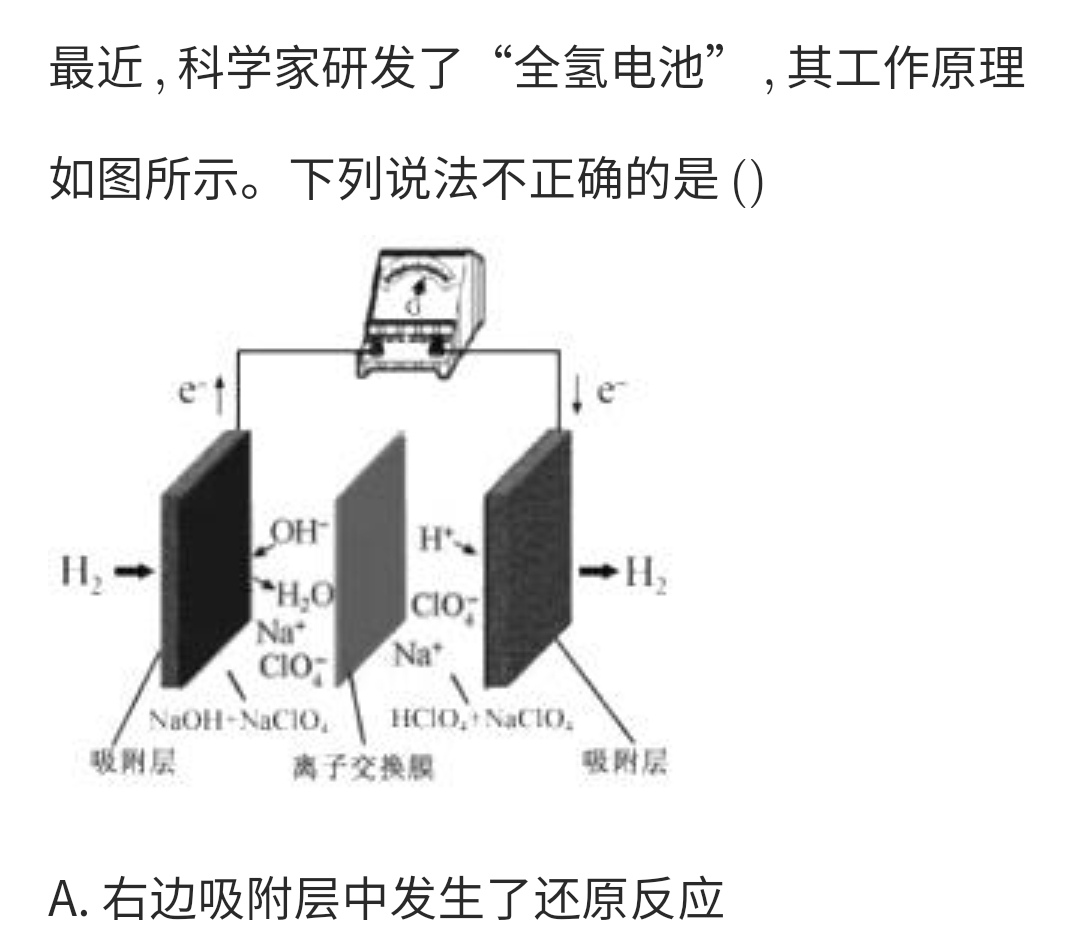
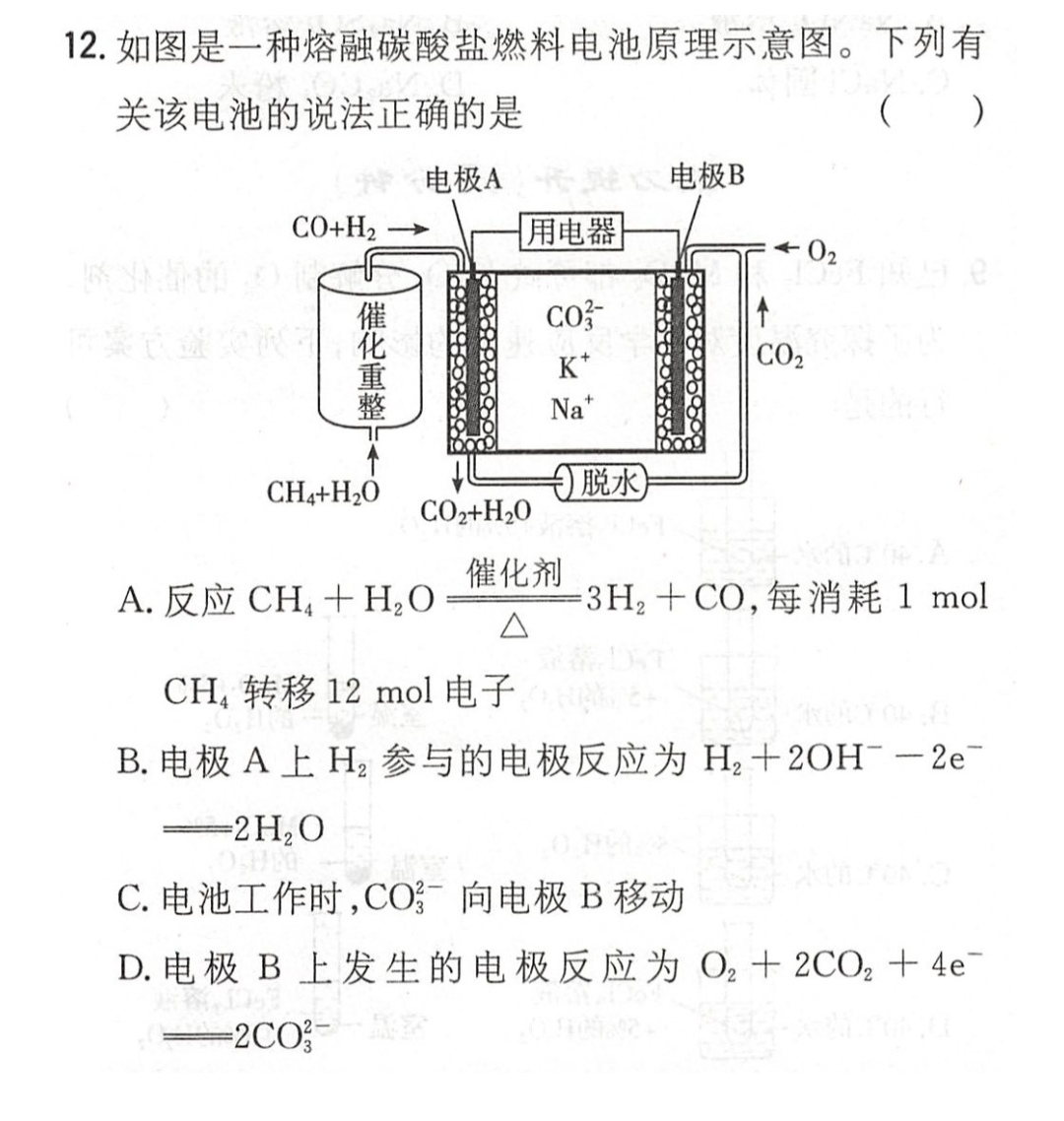
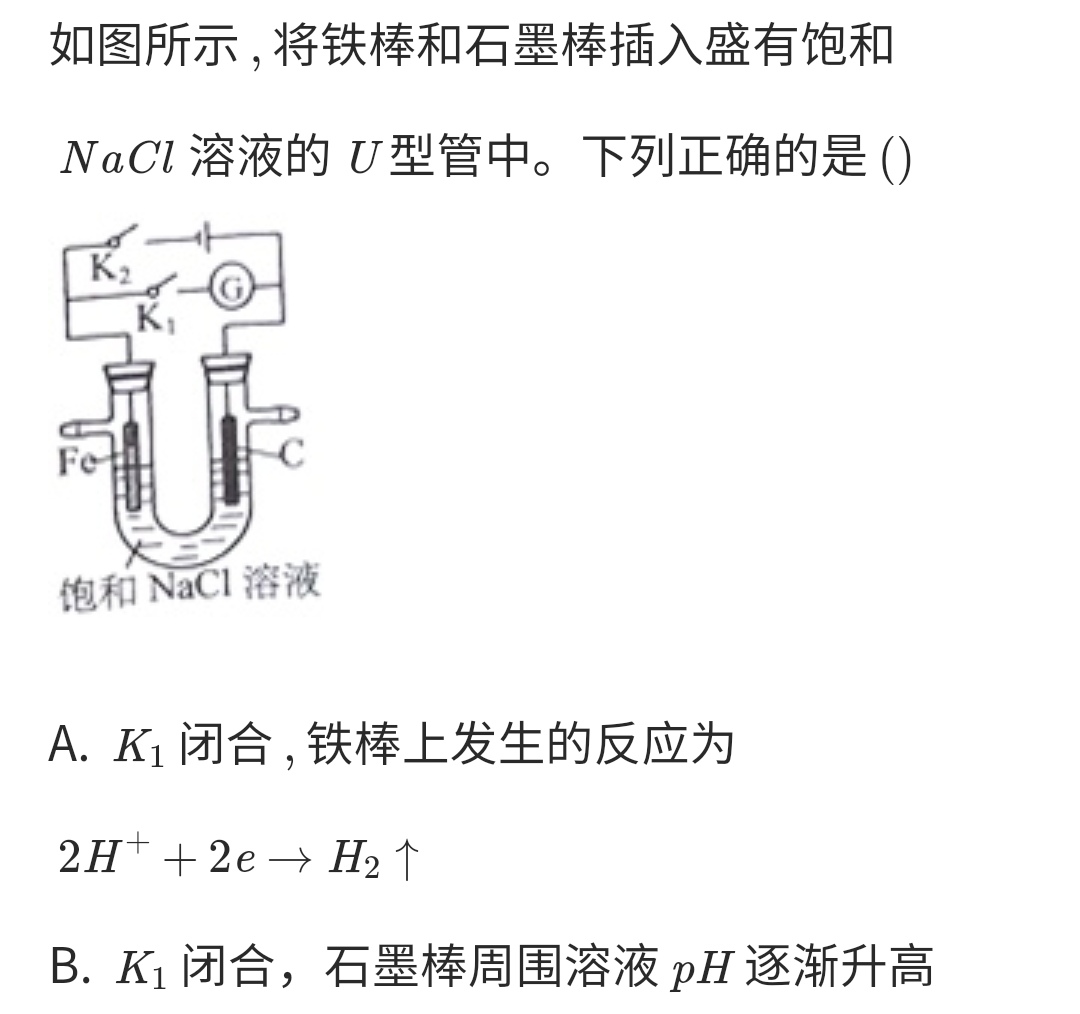
Primary cell and Electrolytic cell
Mnemonic
- The positive electrode and cathode are only responsible for transferring electrons
- Primary cell
- Negative oxidation; positive reduction (负氧正还)
- Positive positive negative negative (正正负负): Positively charged ions flow to the positive electrode, and negatively charged ions flow to the negative electrode.
- Positive increase; negative decrease (正增负减): The pH of positive electrode increases, and the pH of negative electrode decreases. Requirements: no proton-exchange membrane
- Negative electrode: Reducing substances For example: metal, \( H_2 \)
- Positive electrode: Oxidizing substances For example: \( O_2 \) \( Cl_2 \)
- Electrolytic cell
- Anode oxidation; cathode reduction (阳氧阴还)
- The anode is connected to the positive pole, and the cathode is connected to the negative pole
- Anode: producing oxidizing substances
- Cathode: producing reducing substances
- The anode and the cathode attract each other (阴阳相吸): Positively charged ions flow to the cathode, and negatively charged ions flow to the anode.
- The cathode rise and the anode fall (阴盛阳衰): The pH of the cathode increases, and the pH of the anode decreases. Requirements: no proton-exchange membrane
NCEE
Primary cell
Electrolytic cell

Electrode reaction

Redox
Mnemonic
-
失升氧化还原剂,得降还原氧化剂
-
Primary cell and Electrolytic cell
- 留点铁修路 \( S^{2-} > I^{-} > Fe^{2+} > Br^{-} > Cl^{-} > OH^{-} \) -> \( S - I_2 - Fe^{3+} - Br_2 - Cl_2 - O_2 \)
- 印铁通勤 \( Ag^{+} > Fe^{3+} > Cu^{2+} > H^{+} \) -> \( Ag - Fe^{2+} - Cu - H_2 \)
Procedure: 0
When the chemical valences of elements of a substance is difficult to know, they can be marked with 0.
Structure of matter: Electron-dot diagram & Structural formula
The numbers of covalent bonds for Short-period elements (common situation)
(determined by valence electron)
- 1: H F Cl
- 2: O S
- 3: B Al N P
- 4: C Si
- 5: P
- 6: S
- 7: Cl
Exercise
1
Electron-dot diagram of Sodium azide
(No, it is not  . This is illegal in NCEE.)
. This is illegal in NCEE.)
Weak electrolyte
Mnemonic for speed
- Negative Negative Positive Positive: \( X^{+} + H_2O \rightleftharpoons XOH + H^{+} \) \( X^{-} + H_2O \rightleftharpoons HX + OH^{-} \)
Unimportant Procedure 1
\( \frac{v_{postive}}{v_{negative}} = \frac{K}{Q} \)
Proof for example
\( 2NO_2 (g) = 2NO (g) + O_2 (g) \) \( v_{postive} = k_{postive} c^2(NO_2) \) \( v_{negative} = k_{negative} c^2(NO) \cdot c(O_2) \) When balanced, \( v_{postive} = v_{negative} \) \( \frac{k_{postive}}{k_{negative}} = \frac{c^2(NO) \cdot c(O_2)}{c^2(NO_2)} = K \) Other times, \( \frac{v_{postive}}{v_{negative}} = \frac{k_{postive}}{k_{negative}} \cdot \frac{c^2(NO_2)}{c^2(NO) \cdot c(O_2)} = \frac{K}{Q} \)
\( K_h \)
\( K_h = \frac{K_w}{K_a} \)
Proof:
\( K_h = \frac{c(HA) \cdot c(OH^-)}{c(A^-)} = \frac{c(HA) \cdot c(OH^-) \cdot c(H+)}{c(A^-) \cdot c(H+)} = \frac{K_w}{K_a} \)
NCEE

Chinese
Classical Chinese
Statistical conclusion: Multiple choice question of meanings of words
Uncommon words and meanings = correct
Same meaning in modern and classical Chinese = wrong
Different meanng in modern and classical Chinese = mostly correct
Novel
Themes
The unique social environment and values of mainland China form featured themes in examinations.
- Beauty (人性美) and ugliness (人性丑) of humanity
- Beauty: family love (亲情), intimacy (爱情), friendship (友情), national sentiment (民族情) and love with strangers (陌生人情) etc
- Ugliness: arrogant and ignorant (傲慢无知), follow the crowd and trending (从众趋新), complacency (固步自封)
- Complexity (人性的复杂)
- Sympathy and mercy (同情与怜悯)
- War and Peace (战争与和平)
- Anti-war and yearning for peace (反战和对和平的向往)
- Red culture, revolutionary tradition (红色文化 革命传统)
- Thinking of civilization (文明的思考)
- The future of humanity (人类未来): Science and fantasy (科学与幻想)
- Thoughts on the process of urbanization (城镇化进程的思考)
- Thinking of tradition (对传统的思考)
- Changes of the times (时代的变革)
- Human and nature (人类与自然)
- Live in harmony (人与自然和谐共处)
Magic & Reality
Representative Writers: Gabriel García Márquez
Template
- The magic storyline has a basis in reality.
- Magical details are vivid and realistic, with no contradiction to reality.
- Magical things and phenomena symbols, represents and suggests real life.
NCEE
1



2



Poetry
"命蹇词工"
-- The reason
- Youth (青年): make a sightseeing tour (游山玩水); Eager to be used (渴望重用)
- The prime of life (壮年): running for achievements (奔走功名); frustration with career path (失意仕途)
- Old age (暮年): aged with great aspirations (老骥伏枥); feelings about hiding (隐逸情怀)
Themes
- 山水田园 官场黑暗;向往宁静;淡泊名利
- 边塞征战 建功立业;厌战思归;边塞豪情
- 咏史怀古 历史变迁;借古讽今;以古自喻
- 羁旅思乡 孤寂漂泊;思乡思亲;壮志难酬
- 咏物抒怀 托物言志;以物自喻
- 送别劝勉 离愁別绪;豁达豪迈
- 生活杂感 青春易逝;仕途失意;偶得喜悅
Techniques (手法)
Sorted by frequency in NCEE (2010-2020)
- 虚实结合
- 衬托
- 对比
- 借景抒情
- 用典
- 拟人
- 比喻
表达效果常用术语
- 生动形象/化抽象为具体
- 突出了/平添了丰富了...
- 委婉含蓄写出了...
- 化静为动/化虚为实
- 意蕴丰富/贴切自然
- 细致传神地刻画了...
- 具有极强的艺术感染力
- 构思新奇/用词巧妙
Write from memory

論語-MindMap
format: https://markmap.js.org/repl/ https://github.com/gera2ld/markmap
为政以德
以德治国
- 2.1
反对战争,武力,权数,苛政
- 2.3
- 16.1
- 14.5
- 12.19
民本
- 12.9
富民,教民
- 13.9
正己
- 12.7
- 13.6
克己复礼
How
Why
诲人不倦
教育
作用
- 17.3
身教
- 17.19
因才施教
-
11.3
-
11.22
对象
- 15.39
方法
启发诱导式
- 7.8
建立在德行之上
- 3.8
精益求精
- 1.15
Handwriting
It's necessary to have a prefect handwriting for any examinations.
Mathematics
This is a subject that examine students' following skills.
- Comprehension
- Calculate numbers fast and without mistakes just like a old school calculator
- ...
Algebraic substitutions
Trigonometric substitution
Vector
\(a\cdot b+c\cdot d=(a,c)\cdot(b,d)=\left\lvert(a,c)\right\rvert\cdot\left\lvert(b,d)\right\rvert\cdot cos\theta\)
Exercise 1
\(\sqrt{1-x}+2\sqrt{x}\) max
Cauchy–Schwarz inequality
\((\bar a\cdot\bar b)^2\leq\left\lvert\bar a\right\rvert^2\cdot\left\lvert\bar b\right\rvert^2\)
\(x_1x_2+y_1y_2\leq\sqrt{(x_1^2+y_1^2)(x_2^2+y_2^2)}\)
Exercise 1
\(x+2y+3z=3\) Solve \(\sqrt{x}+\sqrt{y}+\sqrt{z}\)
Derivative
Procedure: L'Hôpital's rule
https://web.archive.org/web/20210121123228/https://en.wikipedia.org/wiki/L%27H%C3%B4pital%27s_rule
Exponential & Logarithm
Logarithmic identities
https://en.wikipedia.org/wiki/List_of_logarithmic_identities
NCEE

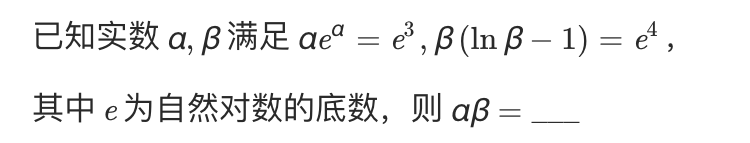
Function
Periodic function
NCEE

2
\( f(x) = 2ax^2+bx-3a+1 \) \( \forall{x} \in [-4,4] . f(x) \geq 0 \) \( 5a+b \) min
Solution
\( f(x) = (2x^2-3)a +xb+1 \)
\( \frac{2x^2-3}{1} = \frac{5}{1} \)
......
\(-\frac{1}{3}\)
Inequality
Procedure: Sugar water inequality
Inequality of arithmetic and geometric means
NCEE
Make Up Proportion
来源: 疑似杭四中
\( x, y, z \in R^+\) 已知 \( x + y + z = 1 \) 求 \( \sqrt{x y} + \sqrt{x z} - y - z \) 的最大值
Solution
\( \sqrt{x y} + \sqrt{x z} - y - z = \sqrt{\lambda x (\frac{1}{\lambda}) y} + \sqrt{\mu x (\frac{1}{\mu}) z} - y - z \leq \frac{\lambda + \mu}{2} x + (\frac{1}{2 \lambda} - 1) y + (\frac{1}{2 \mu} - 1) z \)
\( \frac{\lambda + \mu}{2} = \frac{1}{2 \lambda} - 1 = \frac{1}{2 \mu} - 1 \)
......
\(\frac{\sqrt{3}-1}{2}\)
Taylor series (Maclaurin series)
\(\displaystyle \sum_{n=0}^\infty \frac{f^{(n)}(0)}{n!}x^n\) \(\displaystyle \sum_{n=0}^\infty \frac{f^{(n)}(a)}{n!}(x-a)^n\)
Sometimes the first few terms of the series is used.
Special case 0: Deflation as tangent (放缩为切线)
Number sequence
Procedure
- Given \( a_{n+1} = k a_n + p a_{n-1} \), \( a_{n+1} - x a_n = (k - x) (a_n - x a_{n-1}) \) where \( x^2 = k x + p \)
Procedure: y = x Model
NCEE
数列 { \( a_n \) } 满足 \( a_1 = a \), \( a_{n+1} = a_n^2 + a \) 且 \( \left\lvert a_n \right\rvert \leq 2 \), 则 \( a \) 的取值范围为 ()
A. [-2,2] B. [-2,0] C. [0,\( \frac{1}{4} \)] D. [-2,\( \frac{1}{4}\)]
Scaling
\(a_1\frac{1-q^n}{1-q}\leq\frac{a_1}{1-q}\) where \(q\in(0,1)\)
NCEE


On A Plane ...
Line
General Form: \( A x + B y + C = 0 \) Form 1: \( y = k x + b \)
Theorem 1
\( A x + B y + C \) have the same sign \( \iff \) Points are on the same side
\( A x + B y + C \) have the different sign \( \iff \) Points are on the different side
NCEE

Theorem 2
If the range of angles is continuous
90 degree is in the range and it is not the endpoint \( \iff \) the range of slope is discontinuous
90 degree is in the range \( \iff \) there is \( \infty \) in the expression of the range of slope
NCEE

NCEE: Parallel; Vertical and Auxiliary Rounding




Parametric Equation
Procedure: reflect a point across a line
Given
Line \( Ax+By+C=0 \)
Point 0 \( P_0(x_0,y_0) \)
,
\(d_2=\frac{Ax_0+By_0+C}{A^2+B^2}\)
Point 1 \(x=x_0-2d_2A\) \(y=y_0-2d_2B\)
Circle
\((x-a)^2+(y-b)^2=r^2\)
Tangent:\((x-a)(x_0-a)+(y-b)(y_0-b)=r^2\)
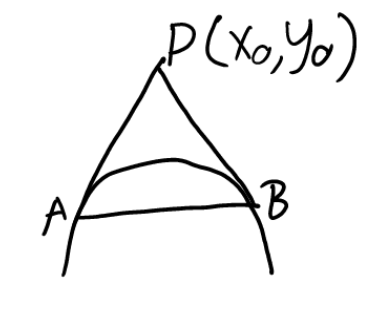
Line AB: \((x-a)(x_0-a)+(y-b)(y_0-b)=r^2\)
NCEE

NCEE: Relations between multiple circles


Ellipse
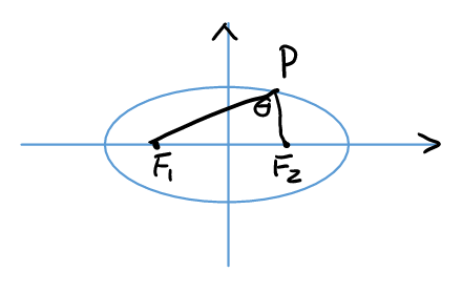
Theorem:
\( S_{\Delta F_1 P F_2} = \frac{1}{2} \left\lvert F_1F_2 \right\rvert \left\lvert y_p \right\rvert = c \left\lvert y_p \right\rvert \)
\( S_{\Delta F_1 P F_2} = b^2 tan \frac{\theta}{2} \)
Theorem 1
\(c\in[sin\frac{\theta}2,1)\)
NCEE


Theorem 2
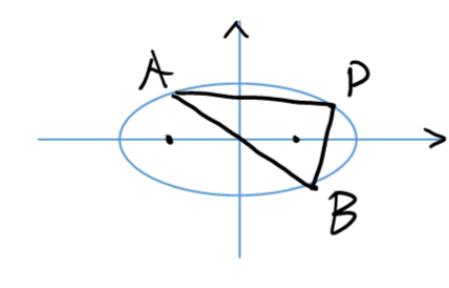
Ellipse/Hyperbola \(k_{PA}\cdot k_{PB}=e^2-1\)
Proof: \(x^2+(\frac{a}{b}y)^2=a^2\) Then regard it as a circle
(or, can alternatively be deduced from point difference method)
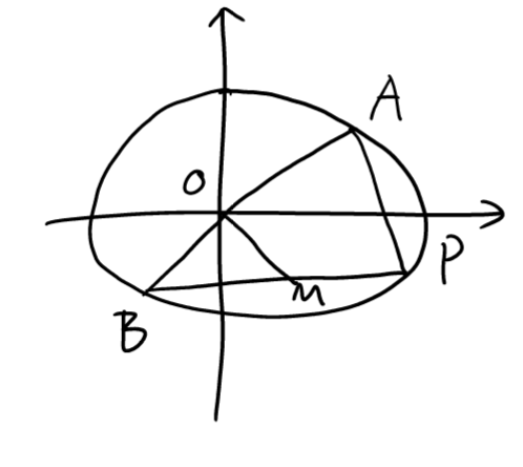
Ellipse/Hyperbola \(k_{MO}\cdot k_{BP}=e^2-1\)
Hyperbola
\( S_{\Delta F_1 P F_2} = b^2 cot \frac{\theta}{2} \)
NCEE

Parabola
Theorem 1
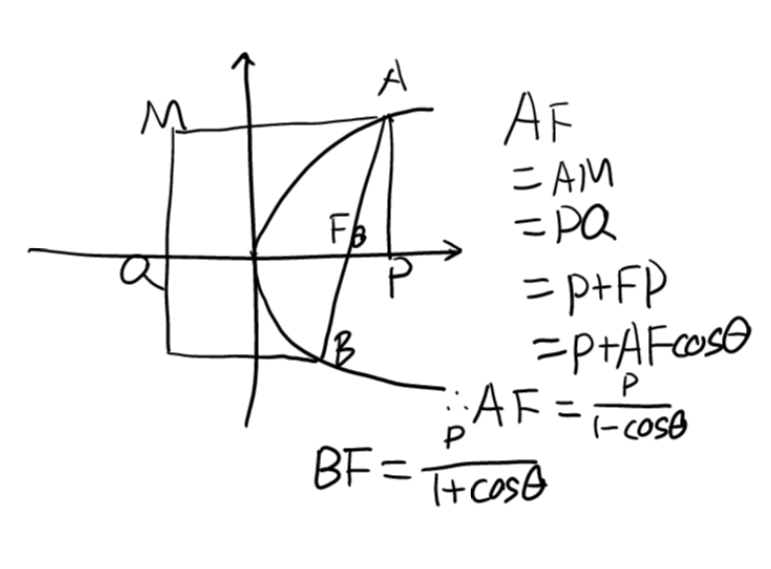 \(AB=AF+BF=\frac{2p}{1-cos^2\theta}=\frac{2p}{sin^2\theta}\)
\(AB=AF+BF=\frac{2p}{1-cos^2\theta}=\frac{2p}{sin^2\theta}\)
Ellipse/Hyperbola: \(AF=\frac{\frac{b^2}a}{1-e\cdot cos\theta}BF=\frac{\frac{b^2}a}{1+e\cdot cos\theta}\)
Parabola/Ellipse/Hyperbola: \(AF=\lambda BF\iff \left\lvert e\cdot cos\theta\right\rvert=\left\lvert\frac{\lambda-1}{\lambda+1}\right\rvert\)
Mnemonic
\(\frac{p}{1\pm\left\lvert cos\theta\right\rvert}\) Long minus;short add
NCEE


设点联立韦达
1
Ellipse:
\(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\) and \(Ax+By+C=0\)
\(\iff\)
\(\Delta=4b^2B^2a^2(a^2A^2+b^2B^2-C^2)\)
\(\Delta'=a^2A^2+b^2B^2-C^2\)
Hyperbola: \(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\iff\frac{x^2}{a^2}+\frac{y^2}{(b i)^2}=1\) so \(\Delta'=C^2+b^2B^2-a^2A^2\)
NCEE

2
\(\alpha x^2+\beta y^2=\gamma\) and \(Ax^2+By+C=0\) \(\iff\) \((\alpha B^2+\beta A^2)x^2+2CA\beta x+\beta C^2-\gamma B^2\)
Ellipse: \(l=\frac{2\sqrt{a^2b^2(A^2+B^2)\Delta'}}{a^2A^2+b^2B^2}\)
Hyperbola: \(l=\frac{2\sqrt{a^2b^2(A^2+B^2)\Delta'}}{\left\lvert a^2A^2+b^2(Bi)^2 \right\rvert}=\frac{2\sqrt{a^2b^2(A^2+B^2)\Delta'}}{\left\lvert a^2A^2-b^2B^2 \right\rvert}\)
Solid geometry
round, sphere
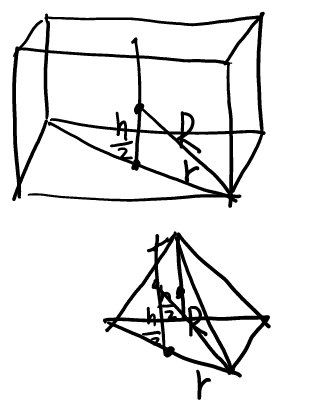
Procedure: Radius of circumscribed sphere
1
\( R^2 = \frac{1}{4} h^2 + r^2 \)
Proof for example:
2
\( R = \frac{l^2}{2} \)
Proof for example:
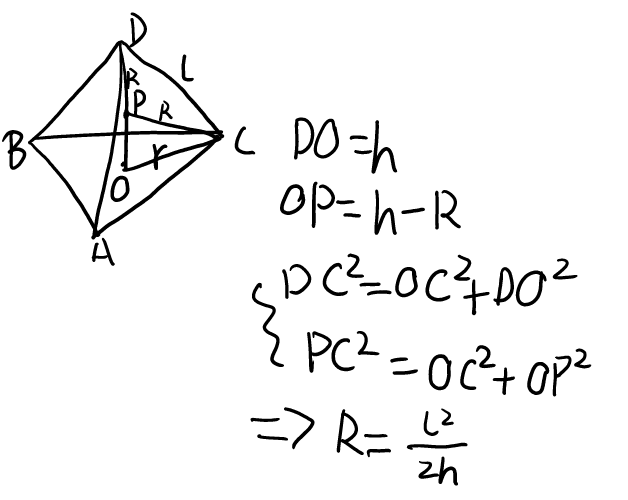
Mnemonic: 两只老虎
Tetrahedron
Opposite sides are equal
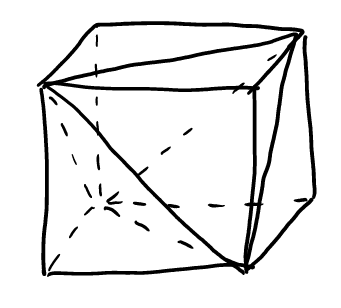
NCEE

Inscribed sphere of a Pyramid
\( R = \frac{3V}{S} \)
Regular tetrahedron with edge length \( a \): \( R = \frac{\sqrt{6}}{12} a \)
normal vector
Procedure: intercept
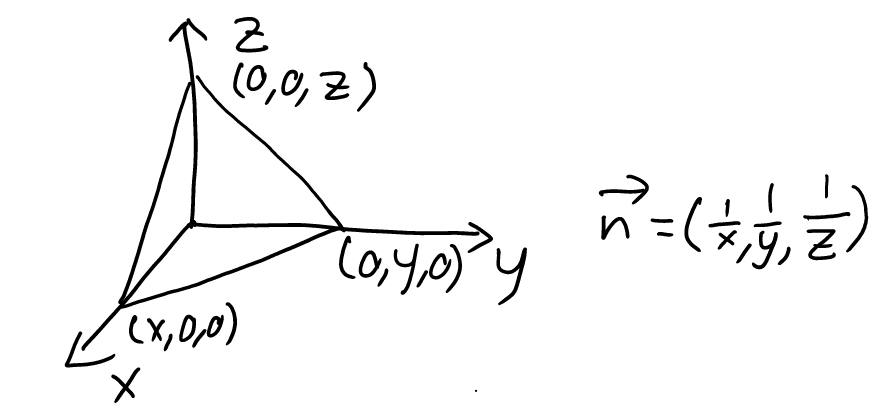
No intersection: For example, \( n = (0, y, z) \) if and only if there is no intersection between the plane and the x-axis.
Procedure: Point-to-Plane Distance
\( \frac{\vec{v}\vec{n}}{\left\lvert n \right\rvert} \)
Procedure: Pyramid Projection
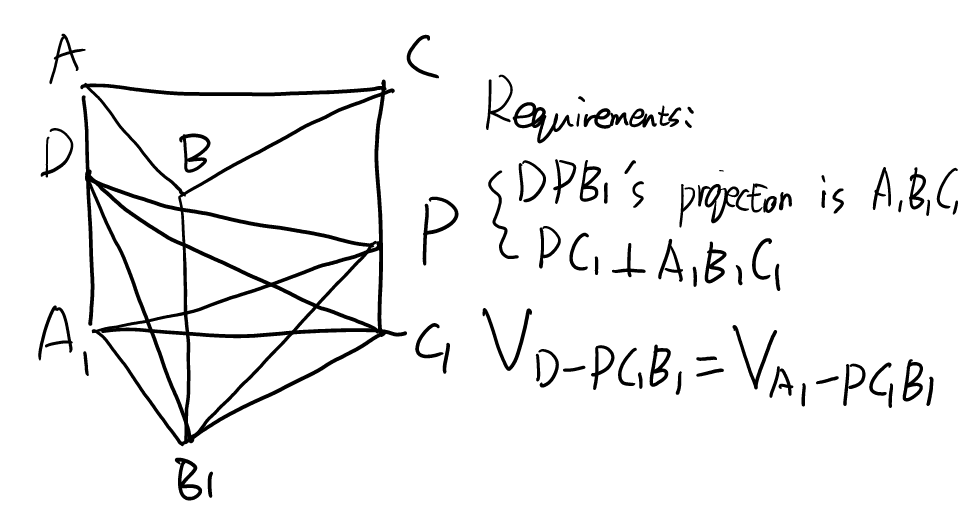
Note: The side edge is perpendicular to the projection surface.
NCEE
Theorem 0
(need more study)
\(sin\alpha=sin\beta\cdot\sin\gamma\) \(\alpha\) 线面 \(\beta\) 锐二面角 \(\gamma\) 线与交线夹角
Statistical Theorem 1
\(V=\frac{4}{3}\pi R^3\)
In general, the radius of the ball is regular which means that radius won't be something like \(\sqrt[3]{\text{...}}\)
NCEE

Some (General?) Methods
Making up Proportion
2

\((x\bar a+y\bar b+z\bar c)^2=...\)
Making up function and number sequence
Construct a constant function or a constant number sequence that satisfies the multiple-choice question whenever possible.
Skip the step of construct \(g(x)\)
......+\(f'(x)\)+.........\(<0 \iff\) \(g'(x) < 0\)
Specific value: 2D -> 1D
Represent the two-dimensional figure described in the multiple-choice question on a one-dimensional line whenever possible.
Statistics & Probability
\( \displaystyle \sum_{i=1}^n (x_i - \bar x)^2 = \displaystyle \sum_{i=1}^n x_i^2 - n \bar x^2 \)
\( s^2 = \displaystyle \sum_{i=1}^n \frac{(x_i - \bar x)^2}{n} = \frac{\displaystyle \sum_{i=1}^n x_i^2}{n} - \bar x^2 \)
NCEE

Trigonometric
Brocard points
NCEE
张角定理
Apollonius's theorem
Physics
Procedure: Multiple choice
Statistical conclusion:
If you can't solve it, just choose D
Conveyor belt
\(Q=E_k\)
Eletric
\(\varphi=k\frac{Q}{R}\)
Eletric Field
Uniform electric Field
Procedure
- In a parallelogram ...

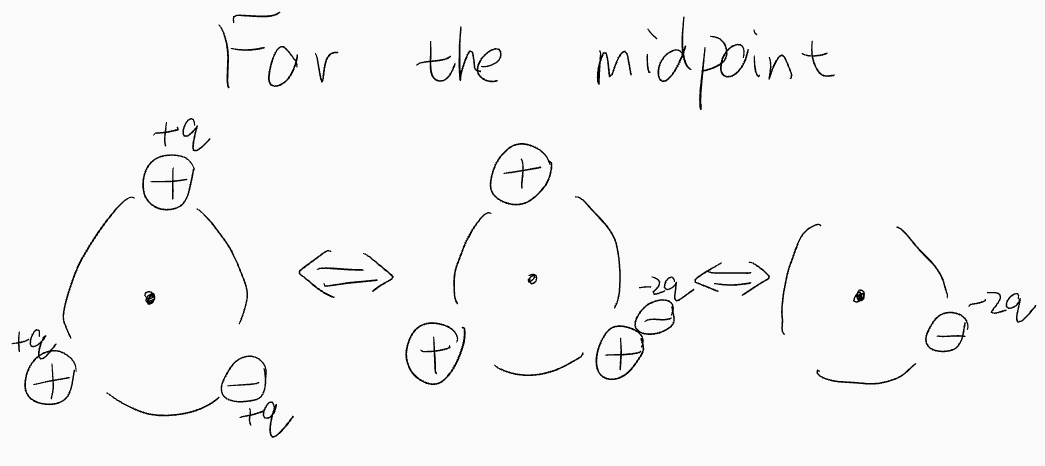
Procedure: Symmetry
NCEE
1

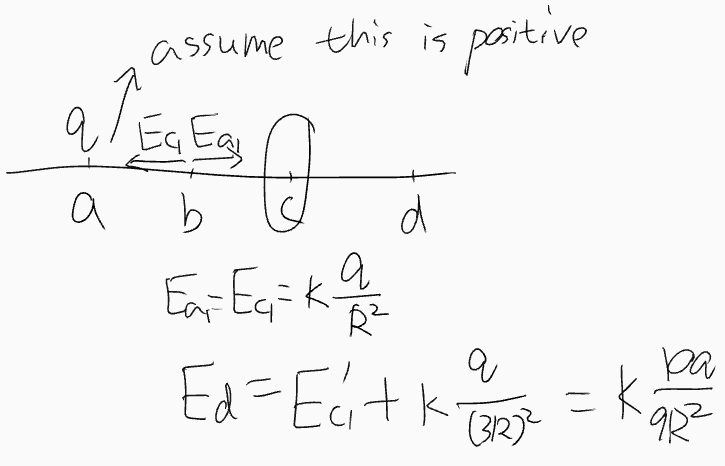
2

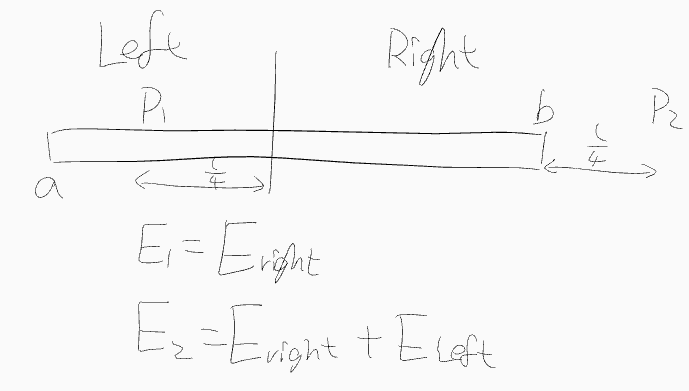
Procedure 2
Capacitor
\( C = \frac{Q}{U} \) \( C = \frac{\epsilon_r S}{4 \pi k d} \)
\( E = \frac{U}{d} \)
Procedure: \( E \propto \frac{Q}{S} \)
Proof: \( E = \frac{U}{d} = \frac{Q}{C \cdot d} = \frac{Q}{\frac{\epsilon S}{4 \pi k d} d} = \frac{4 \pi k Q}{\epsilon S} \)
Alternating Current
Procedure: Equivalent current
- sine, cosine: \( I = \frac{I_{max}}{\sqrt{2}} \)
- Calculate the average of \( I^2 \)
Procedure: Dynamic analysis of the circuit with internal resistance
Components connected in series: Inverted ratio Paralleled: proportional ...
Force
Procedure: Similar triangles
- Geometric triangles are similar to vector triangles
NCEE
1
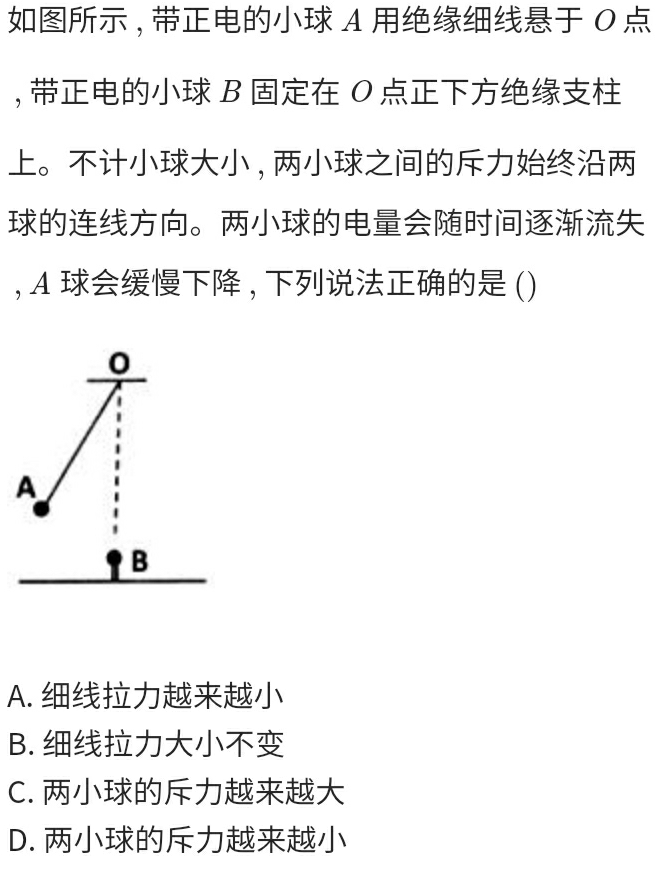
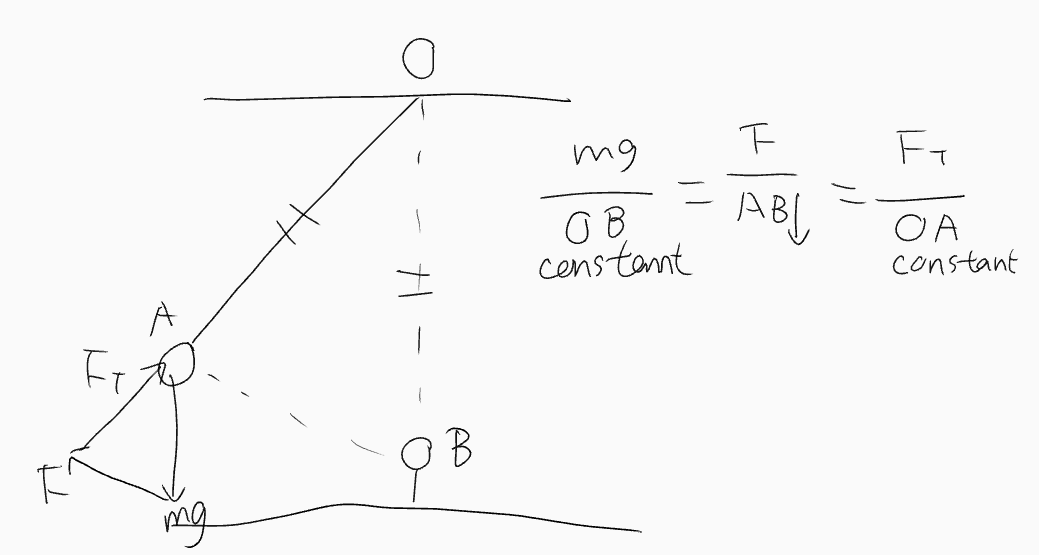
Procedure: Deformed Lever
- Two balls balanced by three forces
- Have a pair of internal forces (e.g., coulombic forces)
- Another pair of forces crossed at one point, which is the fulcrum
NCEE

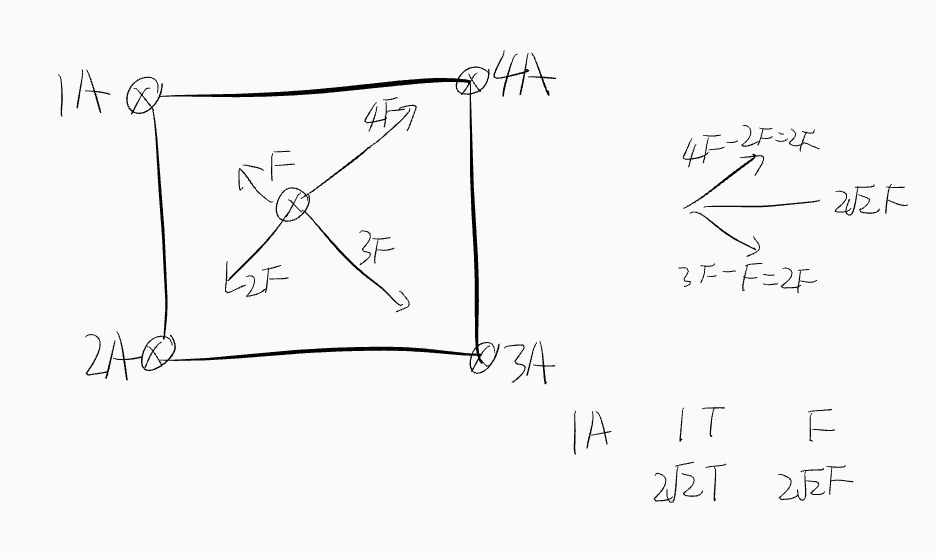
Procedure 3
Requirement: The resultant force of multiple forces is zero
If a force \( F \) is reversed, the resultant force after that is \( 2F \)
Kinetic energy
Work-energy theorem
Procedure: decomposition
one case
Requirement: The speed in one direction is unchanged Explanation: reference frame conversion
Proof for one case: \( \frac{1}{2} m v_1^2 - \frac{1}{2} m v_0^2 = \frac{1}{2} m (\sqrt{v_0^2 + v_y^2})^2 - \frac{1}{2} m v_0^2 = \frac{1}{2} m v_y^2 \)
general
\( F_x = m \frac{v_x^2 - v_{x0}^2}{2x} \)
\( W_x = F_x x = \frac{1}{2}m v_x^2 - \frac{1}{2}m v_{x0}^2\)
Magnetic Field
Procedure: Forces between two currents
Two wires carrying current in the same direction attract each other, and they repel if the currents are opposite in direction.
Procedure: Test Electric Current
Used to analyze the strength of the magnetic field generated by multiple currents.
- Imagine that there is a current at the coordinates to be analyzed
- Calculate the resultant force
- Use Left-hand rule to determine the direction of the magnetic field; \( F \propto B \propto I \)
NCEE
1

Solution
2
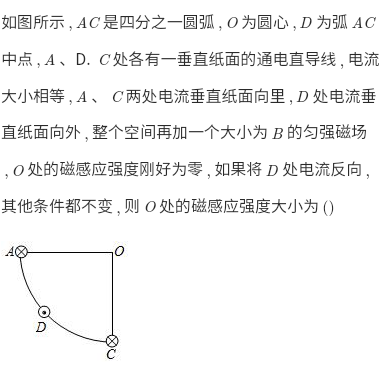
Circular motion
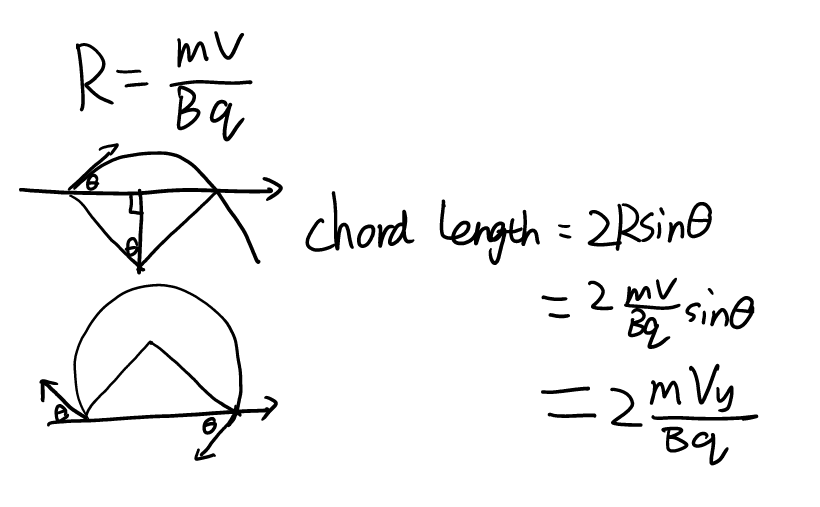
Velocity deflection angle = central angle = 2 * chord tangent angle (or \(2\pi\) - 2 * chord tangent angle)
2
If the point of the center of the circle is on the lines of the enter and/or exit velocities
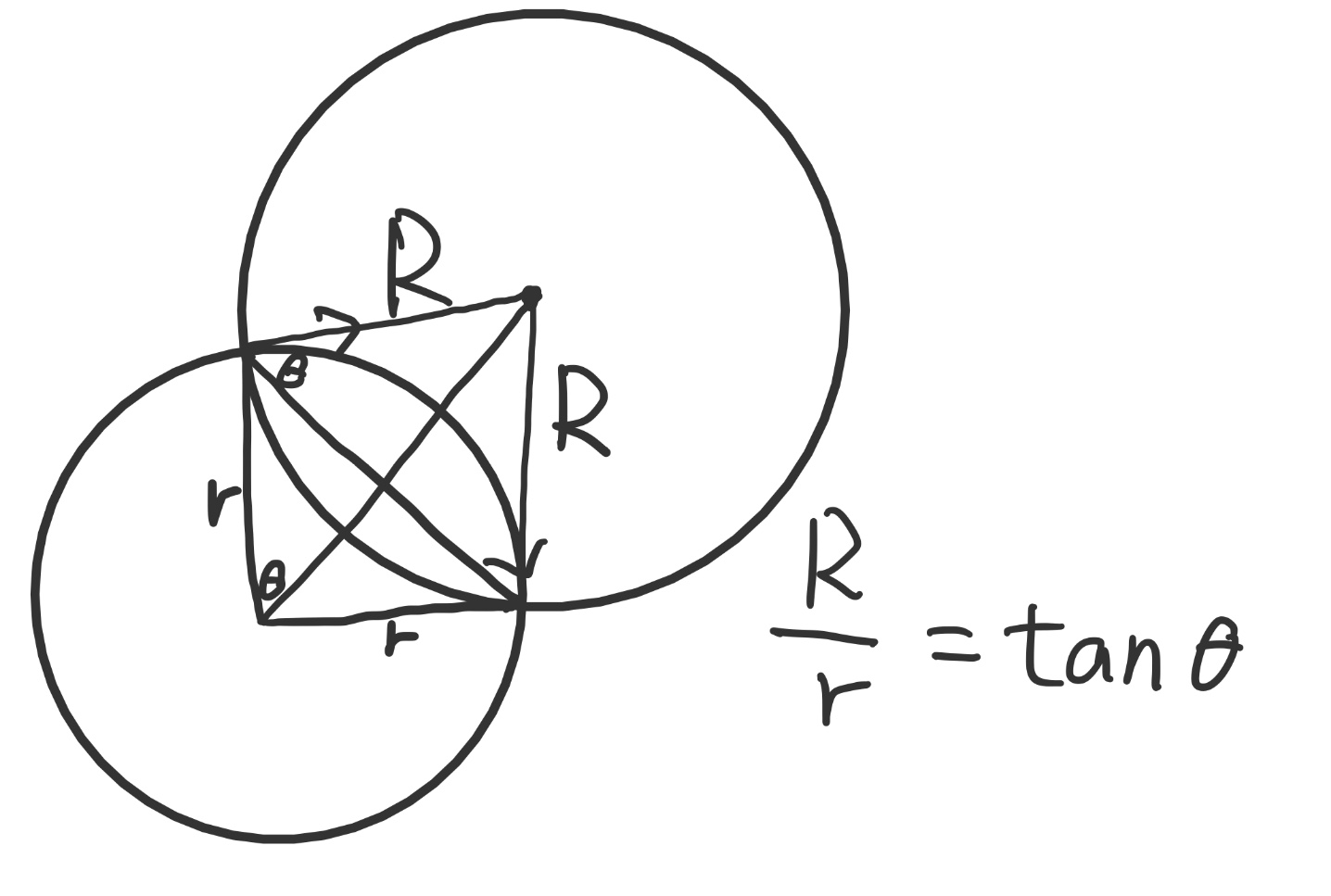
Minimal circle
diameter of the circle = chord length of the motion
area of mimimal rectangle = height of ircular segment * chord length
NCEE

Procedure: Decompose Lorentz force
\( F_x = q(E_x + v_y B_z - v_z B_y ) \)
For NCEE:
\( q l_x B = \Sigma q v_x B t = m \Delta v_y \)
\( q l_y B = \Sigma q v_y B t = m \Delta v_x \)
NCEE

2

Hint: rotate the diagram
Momentum
Perfect Elastic Collision
\( m_1 v_1 + m_2 v_2 = m_1 v_1' + m_2 v_2' \)
\( \frac{1}{2} m_1 v_1^2 + \frac{1}{2} m_2 v_2^2 = \frac{1}{2} m_1 v_1'^2 + \frac{1}{2} m_2 v_2'^2 \)
Procedure
- \( v = \frac{m_1 v_1 + m_2 v_2}{m_1 + m_2} \)
- \(v_1\), \(v\) and \(v_1'\) form an arithmetic sequence. \(v_2\), \(v\) and \(v_2'\) form another arithmetic sequence. (\( v - v_1 = v_1' - v \) and \( v - v_2 = v_2' - v \))
Perfectly inelastic collision
\( m_1 v_1 + m_2 v_2 = (m_1 + m_2) v' \)
Procedure
- \( Q = \frac{1}{2} \frac{m_1 m_2}{m_1 + m_2} (v_1 - v_2)^2 \) (Available energy, deduced from König's theorem)
- Use a special reference frame in which total momentum is zero.
Recoil
Requirement: The total momentum is zero.
Procedure
- Momentum and impulse are equal and opposite.
- \( \frac{a_1}{a_2} = \frac{v_1}{v_2} = \frac{x_1}{x_2} = \frac{E_{k1}}{E_{k2}} = \frac{m_2}{m_1} \)
Collision multiple times
Procedure
- For any collision occurring in an isolated system, momentum is conserved.
- One people throwing a ball at a wall \( I' = I = (2n - 1) m v \) ; \( I' = M v_n \)
- Two people throwing a ball at each other \( I_1 = (2n - 1) m v \) ; \( I_2 = 2n m v \)
NCEE

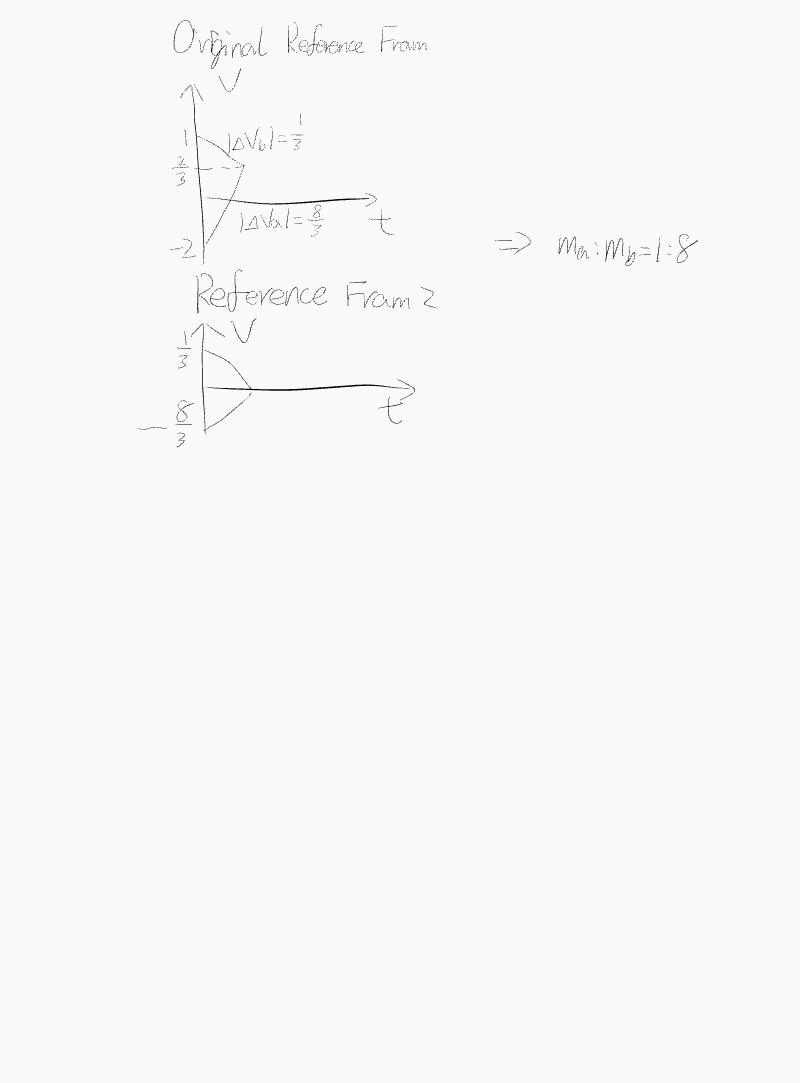
Inelastic collision
Procedure
- \( E_{loss} = \frac{1}{2} \frac{m_1 m_2}{m_1 + m_2} (\Delta v_a^2 - \Delta v_b^2) \) (\( \Delta v_a \): Before collision; \( \Delta v_b \): After collision)
NCEE
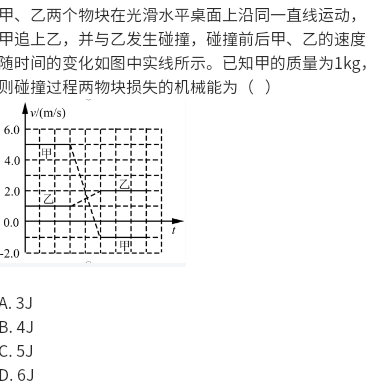
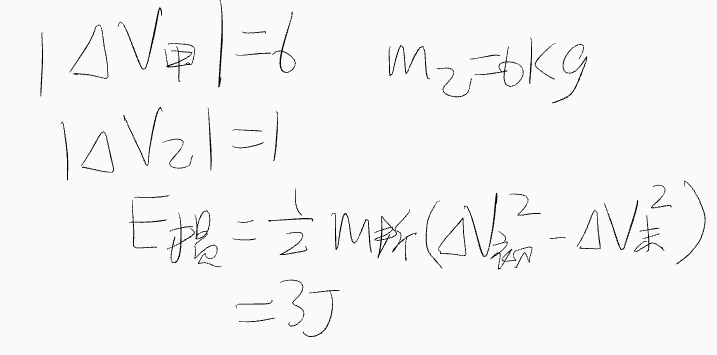
Motion
Uniformly accelerated motion with zero initial velocity
Equal-time displacement ratio 1:3:5:...
Equal-displacement time ratio 1:\(\sqrt{2}-1\):\(\sqrt{3}-\sqrt{2}\):...
If time ratio is \(\frac{1}{2}\):1:1:1:1... , displacement ratio is \(\frac{1}{8}\):1:2:3 or 1:8:16:24:...
Initial and final velocity being zero
\(\frac{t_1}{t_2}=\frac{x_1}{x_2}=\frac{a_2}{a_1}\)
If \(ma_1=(F-f)\) and \(ma_2=f\), \(\frac{F}{f}=\frac{t_1+t_2}{t_1}=\frac{x_1+x_2}{x_1}\)
Equal-time return
\(x_1:x_2=1:1\) \(v_1:v_2=1:2\) \(a_1:a_2=1:3\)
Movement
Parabola
Curved motion with constant acceleration
Note: Sometimes the speed cannot decease to 0.
Procedure: Newton's second law of The whole system
\( F_x = m_1 a_1x + m_2 + a_2x + ... \)
Exercise
1
Solution
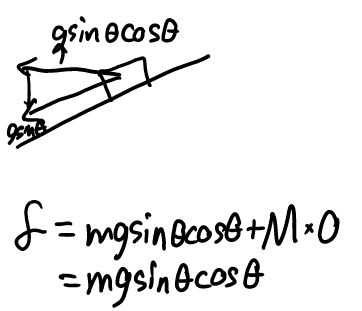
Procedure 2
\( \left\lvert \frac{F_x}{F_y} \right\rvert = \left\lvert \frac{\Delta v_x}{\Delta v_y} \right\rvert \) (deduced from impulse-momentum theorem)
Horizontal cast movement

\( y = \frac{1}{2} a t^2 = \frac{1}{2} a (\frac{x}{v_0})^2 = \frac{F}{2m v_0^2} x^2 = \frac{F}{4E_{k0}} x^2 \)
\( tan \theta = y' = \frac{F}{m v_0^2} x = \frac{F}{2E_{k0}} x \)
\( tan \theta_v = 2 tan \theta \)

